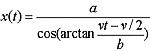| Google překladač: |
|
|
Exkluzivní partner sekce
Aktuality
- JLR a Dassault rozšiřují partnerství
- Pozvánka na SOLIDWORKS STAHLBAUTAG 2024
- Siemens oznamuje NX X pro produktové inženýrství
- Konference 3DEXPERIENCE 2024 v Mnichově
- Eurotech zařazen do Gartner Magic Quadrantu
- Digitální simulace je rychlejší než fyzické prototypy
- Siemens prodá Innomotics firmě KPS Capital Partners
- EMO Hannover 2025 bude zkrácen na 5 dnů
CAD na www.SystemOnLine.cz
3D tisk kovů je nová výzva a trend, ale především výrazná konkurenční výhoda
Novinka od Sony pro tvůrce 3D obsahu
3D tisk bude nedílnou součástí budoucnosti obuvnictví
Jak se bude vyvíjet 3D tisk v roce 2024T+T Technika a trh
Umělá inteligence a kyberbezbečnost
Jak CNC řezací plotr KIMLA našel uplatnění ve výrobě kabinv DFK CAB
RAVEO nově spolupracuje s Reggiana Riduttori
Společnost InnovMetric představuje PolyWorks 2024
Generace Z na pracovním trhuStreamTech.tv
Deskriptivní geometrie – jádro CAD systémů |
| Úterý, 01 Prosinec 2009 09:41 | |
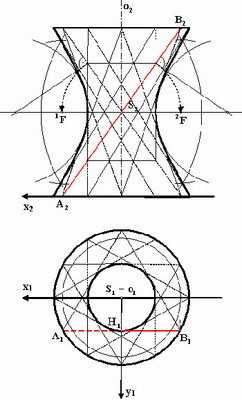
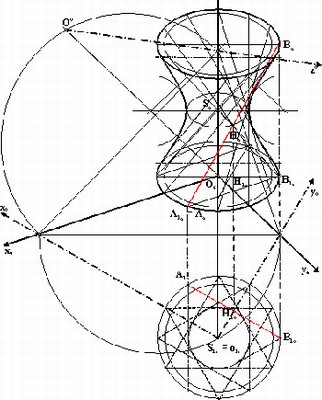
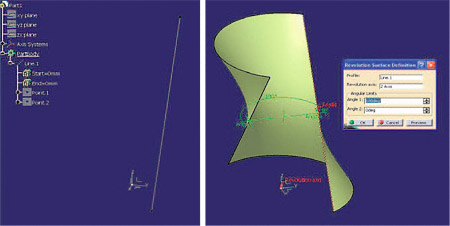
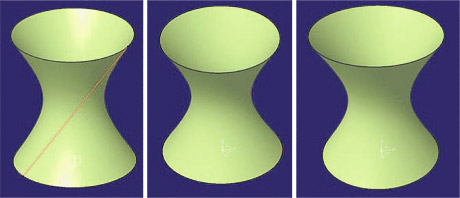
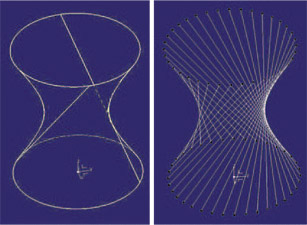
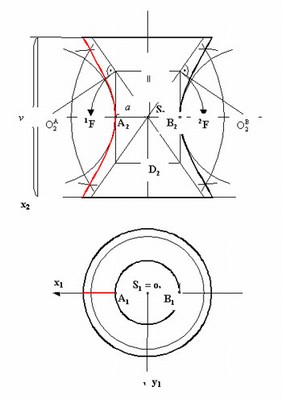
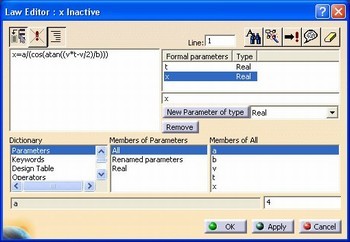
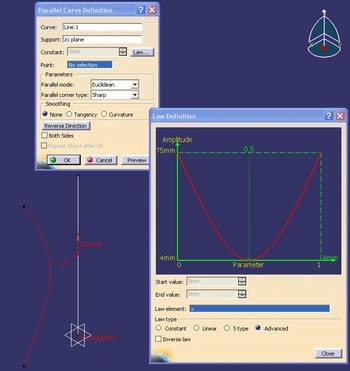
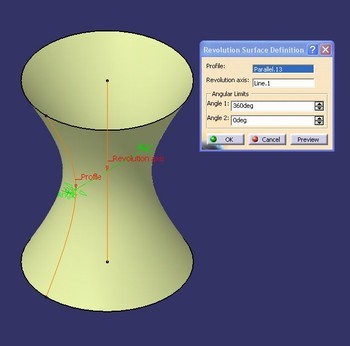
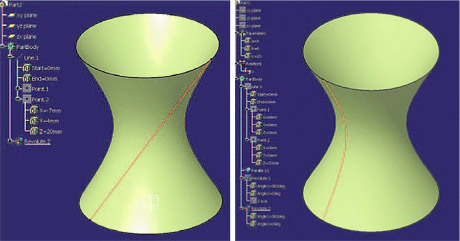
![McDonnell planetarium, Saint Louis, USA [4]](/images/stories/clanky/2009/03/03-deskriptiva.jpg "McDonnell planetarium, Saint Louis, USA [4]") My dříve narození absolventi středních odborných škol a vysokých škol technického směru jsme prošli výukou deskriptivní geometrie. S nástupem CAD systémů lze pozorovat trend odbourávání výuky deskriptivní geometrie z učebních osnov. Jsou tato rozhodnutí správná? Nepřipravujeme se o teorii prostorového vidění? Opravdu mohou CAD systémy nahradit tuto nauku, jejíž rozvoj se datuje do dob starověké Mezopotámie? Dost bylo otázek, nechme hovořit fakta historie, ale i fakta současnosti a snažme se společně hledat odpovědi na naše otázky.Trocha historieGeometrie je jedna z nejstarších matematických disciplín. Její počátky sahají do starověké Mezopotámie, Egypta, Řecka a Říma. Pravděpodobně nejstarším zachovaným dokladem rýsování je kamenná destička z r. 4000 př. n. l., na níž je zobrazen půdorys pevnosti. Významnou roli hraje geometrie ve starém Egyptě, kde díky pravidelným záplavám museli zeměměřiči stále znovu vyměřovat pozemky, počítat jejich obsahy a obvody. Délku kružnice a obsah kruhu počítali podle vzorců, které používáme dodnes. Deskriptivní geometrieVýtvory techniky jsou vždy prostorové. Navrhujeme je a zobrazujeme rovinným nákresem – technickým výkresem. Na sestrojování technických výkresů je mnoho pravidel, jejichž podstatná část je shrnuta v normách. Tyto se však téměř nedotýkají nejdůležitějších pravidel technického výkresu – podstaty zobrazování.Metodami umožňujícími zobrazovat prostorové objekty na rovinu se zabývá samostatné vědecké odvětví – deskriptivní geometrie. Zobrazovací metody nazýváme promítání. Známe dva základní druhy: středové promítání, rovnoběžné promítání. Při středovém promítání všechny promítací paprsky procházejí jedním bodem – středem promítání (obr. 1). Speciálním případem středového promítání je lineární perspektiva, která vytváří nejreálnější obraz zobrazovaného objektu. 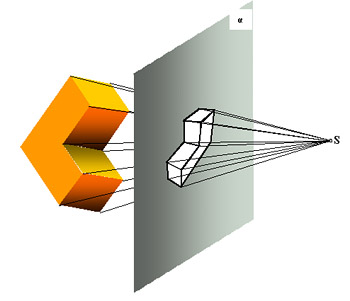 Obr. 1 Zobrazení objektu ve středovém promítání Při rovnoběžném promítání jsou promítací paprsky rovnoběžné s daným směrem s. Pokud je směr s kolmý na průmětnu, hovoříme o kolmém (pravoúhlém) promítání. Nejčastěji využívanými kolmými promítáními jsou Mongeova projekce a kolmá axonometrie. První z nich, Mongeova projekce, je kolmé promítání na dvě na sebe kolmé souřadnicové roviny karteziánského souřadnicového systému, které sdružíme do jedné nákresny. Získáváme tedy dva kolmé průměty jednoho objektu – půdorys (pohled shora) a nárys (pohled zepředu) (obr. 2). Využitím dalších pomocných průměten můžeme podle potřeby získat další pohledy na objekt (obr. 3). Promítání je vhodné při zobrazování geometrických útvarů v případě, že potřebujeme zachovat jejich měřitelnost. 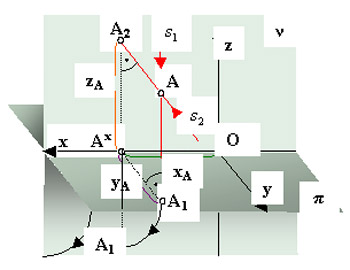 Obr. 2 Zobrazení bodu v Mongeově projekci 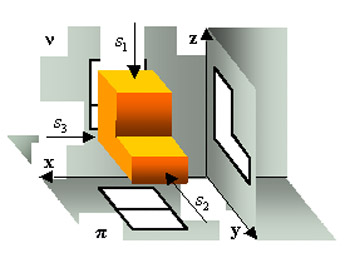 Obr. 3 Tři pohledy na objekt – kolmé průměty do tří rovin v Mongeově projekci Názornější představu o zobrazovaném objektu poskytuje kolmá axonometrie. Při tomto zobrazení promítáme objekt spolu se souřadnicovým systémem do nákresny, přičemž polohu nákresu volíme tak, aby se souřadnicové osy promítly do tří různých přímek (obr. 4). 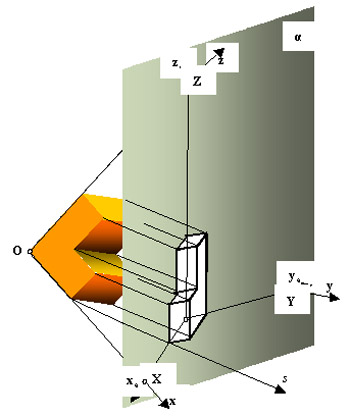 Obr. 4 Axonometrický průmět objektu Při tvorbě technických výkresů je nejčastěji používána Mongeova projekce, neboť jejich podstatnou složku tvoří půdorysné řezy, čelní a boční pohled objektu, což jsou vlastně průměty v Mongeově projekci. Za účelem upřesnění představy o zobrazovaném objektu se využívá jeho axonometrický nebo perspektivní průmět. Tématem dalšího textu bude pojednání o konstrukci a zobrazení šikmého prizmatické tělesa (šestiboký šikmý hranol) a o konstrukci rotačního tělesa (jednodílný rotační hyperboloid) syntetickými metodami deskriptivní geometrie a s pomocí 3D CAD systému CATIA V5. Šestiboký šikmý hranolPředpokládejme hranol, jehož podstava je pravidelný šestiúhelník se středem S a vrcholem A, ležící v souřadnicové rovině (xy). Osou hranolu je přímka SS'.Zobrazení tohoto tělesa v Mongeově projekci je jednoduché (obr. 5). Při kolmém průmětu do roviny (xy) se dolní i horní podstava zobrazí jako pravidelné šestiúhelníky a hrany tělesa budou rovnoběžné s osou tělesa. Kolmé průměty obou podstav do roviny (xz) jsou úsečky. Hrany se znovu zobrazí rovnoběžně s průměty osy. 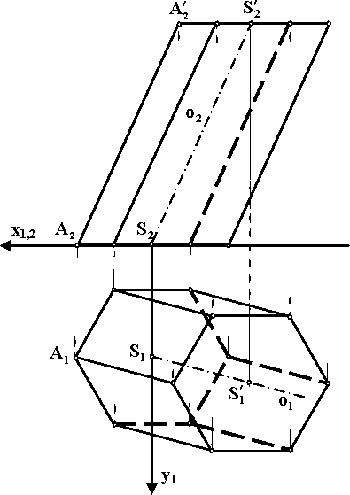 Obr. 5: Půdorys (pohled shora) a nárys (pohled zepředu) šikmého šestibokého hranolu Zobrazení tělesa v kolmé axonometrii je už složitější. Průmět podstavy sestrojíme využitím afinního vztahu dvou rovinných polí. V otočené rovině (xy) nejprve sestrojíme půdorys podstavy jako v Mongeově projekci a pomocí osové afinity sestrojíme její axonometrický průmět (obr. 6). Hrany tělesa se zobrazí rovnoběžné s průmětem osy SS' (obr. 7). 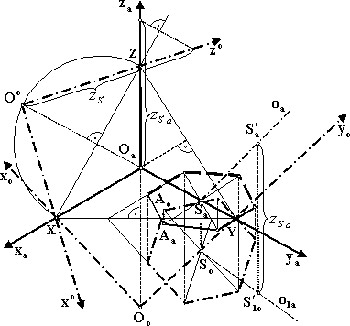 Obr. 6 Zobrazení podstavy tělesa v kolmé axonometrii 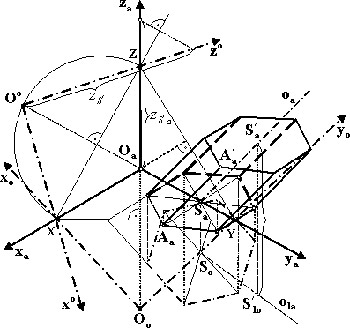 Obr. 7 Axonometrický průmět šikmého šestibokého hranolu Na základě výše uvedeného zadání namodelujeme šestiboký šikmý hranol v objemovém modeláři CAD systému. Modelování bude probíhat v prostředí Part Design objemového modeláře CATIA V5. Cílem nebude popsat proces „krok za krokem“, ale spíše poukázat na to, že po pár kliknutích myší a zadáním parametrů z klávesnice je „zhmotněn“ matematický popis geometrie objektů a principy deskriptivní geometrie ve 2D a 3D naprogramované kdesi v jádru každého CAD systému.  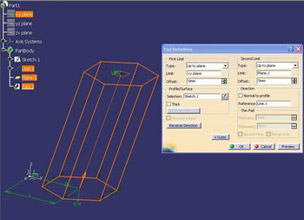 Obr. 8 Postup vytvoření šestibokého šikmého hranolu v Part Design CATIA V5 Tento hranol vzniká na základě skici šestiúhelníka vytvořeného v prostředí skicáře v rovině (xy) a jeho vytáhnutí ve směru čáry SS' . Šestiúhelník je vepsaný do kružnice o poloměru R=|SA|. Konstrukce je velmi jednoduchá a dialog softwaru je velmi intuitivní. Na následujících obrázcích jsou různé způsoby zobrazení daného hranolu, jako např. drátěný model v axonometrii s průměty do průměten (yz), (xz) – (obr. 9) a objemový model v axonometrii a perspektivě (obr. 10). 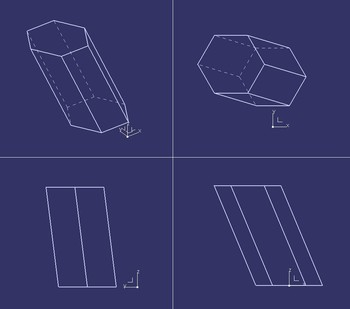 Obr. 9 Axonometrický pohled s viditelností skrytých hran a průměty hranolu 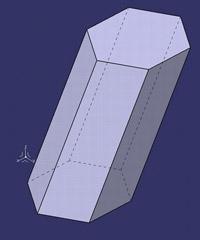 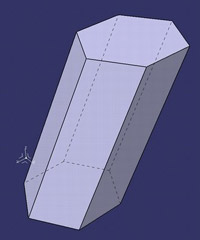 Obr. 10 Axonometrický pohled a perspektivní pohled Rotační jednodílný hyperboloidPopíšeme dva způsoby vzniku této plochy. kde Hledání ekvivalentů deskriptivní geometrie a CADPorovnáním těchto dvou přístupů k zobrazení prostorových objektů docházíme k závěru, že počítač je dobrý pomocník, který nám umí usnadnit a zrychlit práci, dokonce umožňuje nakreslit plochy či křivky, které bychom metodami syntetické geometrie nakreslit nedokázali, ale stále kdesi v podvědomí využíváme již získané znalosti z geometrie. Kdo dostal základy deskriptivní geometrie, vidí v každém grafickém výstupu z počítače i tu geometrii v něm skrytou. Ví, že obrázek ve skicáři je v těchto úlohách vlastně půdorys, pohled znamená nárys nebo bokorys. To vše je Mongeova projekce. Axonometrie že je rovnoběžné promítání, ve kterém platí určité zákonitosti, perspektiva zase středové promítání, ve kterém platí jiné zákonitosti. Na základě těchto znalostí umí posoudit, zda objekt, který počítač nakreslil, odpovídá stanoveným požadavkům. Ne náhodou jsme jako ukázku vybrali rotační jednodílný hyperboloid. Jednak je to krásná a velmi často využívaná plocha v architektuře (obr. 21), ale důvod byl tentokrát jiný. Jak vlastně vznikl náš článek? Na začátku byla plocha v CAD, která se tvářila jako hyperboloid. CAD specialista byl spokojen, dokud nenarazil na geometra. Ten ho usvědčil z omylu a přivedl na správnou cestu. Ale to vše bylo možné jen díky tomu, že geometrie ještě žije.ZávěrNastal čas odpovědět si na otázky položené v úvodu. Nejlepší je, když si na tyto otázky každý odpovídá sám, ale přesto bychom jako autoři rádi vyjádřili nějaké postřehy, které jsme zaevidovali během psaní tohoto článku. Jeden z autorů je učitel deskriptivní geometrie a druhý CA.. odborník. Po této spolupráci musíme konstatovat, že CAD systém je syntézou deskriptivy a matematiky, ukrytou za pomoci analytiků a programátorů v jádru každého CADu. Využívat CAD systém v celém spektru od tvorby základních objemových těles až po modelování na bázi parametrických rovnic se dá využít jen s velmi dobrými základy deskriptivní geometrie a znalostí matematického popisu geometrických objektů. CAD systémy nám mnoho věcí zjednoduší, mnoho věcí je předprogramovaných a zautomatizovaných, ale to, co chceme navrhnout, se musí zhmotnit v prostorovém vidění naší mysli. Staří Egypťané, Řekové a Římané se nemusí obávat, jejich geometrické konstrukce jsou zakódovány v jádrech CA.. systémů. Ale přesto k plnému pochopení konstrukcí starověkých géniů a tím i k efektivnímu využití CA.. systémů je na začátku přece jen potřebná tužka, kružítko a sada trojúhelníků. Po této lekci můžeme sebevědomě vykročit k navrhování pomocí CA.. technologií a tvořit sofistikovaná technická díla.Literatura[1]Madáč, K., Molnár, V., Fedorko, G.: Základy aplikácie Pro/Engineer v technickej konštrukcii. Edičné stredisko AMS, F BERG, TU Košice, 2003 Článek byl vypracován v rámci řešení projektů:
Mohlo by vás zajímat:
|
