Partneři Projektu CAD
- 02.03. AutoCAD – kurz pro pokročilé
- 02.03. Autodesk Fusion 360 – základní kurz (úvod do parametrického modelování)
- 02.03. AutoCAD kurz – navrhování a správa dynamických bloků
- 03.03. Autodesk Fusion 360 – pro uživatele Autodesk Inventor
- 04.03. AutoCAD a AutoCAD LT – základní kurz
- 05.03. AutoCAD 2013 - základní kurz
- 05.03. workshop Strukturální mechanika v programu COMSOL Multiphysics
- 09.03. Autodesk Inventor – návrh trubek a potrubí (Tube and Pipe Design)
- 09.03. Trimble SketchUp – prezentace návrhů
- 10.03. Autodesk Inventor – kurz pro pokročilé (sestavy a strojní návrhy)
Aktuality
- AI na veletrhu HANNOVER MESSE: Od teorie k praxi
- Dassault Systèmes jmenuje nového předsedu představenstva
- HTC VIVERSE spouští nový VIVERSE Partner Program
- FinalWire vydává software AIDA64 v8.25
- Zoo představuje Zookeeper Agent pro CAD návrh
- Pevně zakódovaná budoucnost autonomních továren
- Dell Technologies a McLaren Racing prodlužují spolupráci
- Co je nového v SOLIDWORKS PDM
Využití principů fuzzy množin v geografických IT - Aplikace v území okolí plánované R55 u Bzence |
| Autor článku: Kominácká, J., Peloušková, L. |
| Pátek, 16 Listopad 2012 00:00 |
|
Termíny fuzzy logika a fuzzy množina jako první použil profesor informatiky Lotfi Asker Zadeh na Kalifornské univerzitě v Berkeley v roce 1965 (Zadeh, 1965). Fuzzy logika vychází z poznatku, že v reálném světě nemusí být stavy (černá/bílá, tma/světlo) vždy jednoznačně dány, ale že existují i „mezihodnoty". Fuzzy logika spočívá v rozšíření klasické teorie množin na fuzzy množiny. Teorie fuzzy množin zavedla nový pojem, tzv. stupeň příslušnosti prvku k množině, který využívá všech hodnot v intervalu < 0; 1 >. V obecné teorii množin buď prvek do dané množiny patří, nebo nepatří. Takovou množinu nazýváme ostrou množinou. Tímto způsobem můžeme jasně indikovat, zda daný prvek patří, nebo nepatří do dané množiny. Pokud bychom však připustili určitý stupeň nejistoty z hlediska toho, zda prvek do množiny náleží, můžeme vyjádřit příslušnost prvku k množině jeho funkcí příslušnosti. Funkce příslušnosti přiřazuje každému prvku stupeň náležitosti (příslušnou hodnotu) k fuzzy množině. Tato hodnota musí být mezi 0 a 1 (0 znamená, že nenáleží do dané množiny, 1 znamená, že zcela náleží do dané množiny). Hodnoty mezi 0 a 1 značí, jakou mírou prvky patří do dané fuzzy množiny (Kainz, 2007).
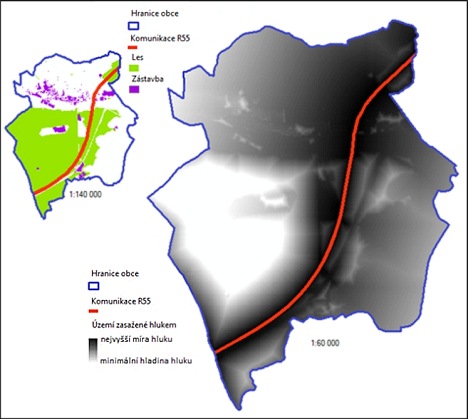
Důležitou liniovou vrstvou je plánovaný záměr rychlostní komunikace R55. Na této vrstvě je demonstrováno šíření hluku a smogu od komunikací a je vyhodnocen dopad na zastavěné území obce. Nad vrstvou plánované rychlostní komunikace R55 je provedena fuzzifikace šíření hluku a smogu od komunikace. Hodnoty používané při provádění analýz jsou stanoveny na základě studie, kterou zpracovala Projektová kancelář pro dopravní a inženýrské stavby (HBH Projekt) Brno ve spolupráci s Ředitelstvím silnic a dálnic ČR. V této studii je také uvedena prognóza intenzit dopravy na posuzované silniční komunikaci R55, kterou zpracovala firma ADIAS Brno (HBH Projekt, ŘSD, 2005). Hluk způsobený dopravou je závislý na několika faktorech přímo ovlivňujících jeho intenzitu. Na eliminaci hluku od komunikace má velký vliv samotný terén krajiny, kde např. kopce šíření hluku znatelně zastaví. Stejně tak lesní porost či zástavba slouží jako bariéra v šíření hluku od komunikace. Více o šíření a dopadu hluku na životní prostředí například v publikaci Hlavni (Hlavňa, 1996). Zdrojem emisí do volného ovzduší v okolí komunikací je provoz motorových vozidel. Na šíření smogu od dopravní komunikace mají stejně jako na šíření hluku vliv zejména povětrnostní podmínky, krajinný reliéf a také teplotní inverze. Do analýzy jsou zahrnuty vrstvy lesů a celková vrstva zástavby. Rasterizovanou vrstvu lesů i budov je nejprve potřeba reklasifikovat. Pomocí reklasifikace je jak vrstvě lesů, tak vrstvě budov nastavena hodnota pohlcování hluku a poté smogu. Obě dvě vrstvy jsou tedy reklasifikovány dvakrát. Pro pohlcování hluku od silniční komunikace je vrstvě budov nastavena dvojnásobná hodnota než vrstvě lesů. Při pohlcování smogu je reklasifikace provedena naopak. Tedy vrstvě lesů je nastavena dvojnásobná pohlcovací schopnost smogu než vrstvě budov. Tímto způsobem vznikly celkem čtyři nové vrstvy. Dále se pomocí nástroje mapové algebry sečtou vrstvy budov a lesů tak, že jedna výsledná vrstva bude zohledňovat, jak budovy a lesy eliminují šíření hluku. Druhá vrstva z mapové algebry zohledňuje, jak les a budovy eliminují šíření smogu od komunikace.
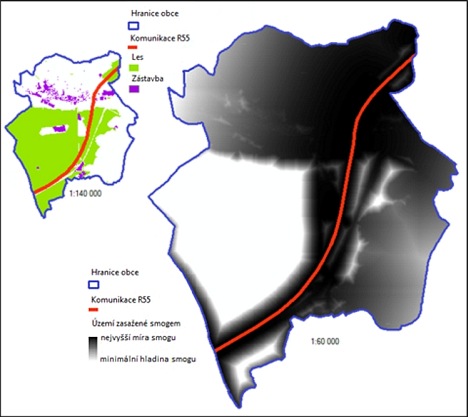
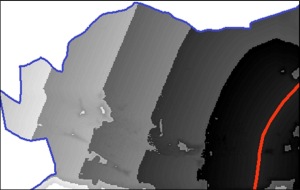
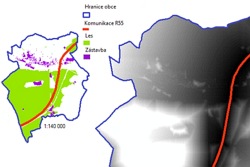
Výsledky mapové algebry mohou obsahovat drobné chyby způsobené nepřesností rasterizace vektorových vrstev. Výsledné vrstvy z mapové algebry je nutné znovu reklasifikovat, a to tak, že každá špatně sečtená hodnota je reklasifikována na správnou hodnotu. Obrázek 1 znázorňuje fuzzifikovanou vrstvu šíření hluku s překážkami ve formě lesů a budov od rychlostní komunikace R55. Na rozdíl od klasického přístupu (klasifikace do tříd), který šíření hluku znázorňuje ostrými přechody, modeluje fuzzy přístup šíření hluku plynulými přechody bez ostrých hranic, a tak více odpovídá skutečnému šíření hluku. Černá místa zobrazují vysokou míru hluku, přičemž bílá barva značí minimální míru hluku. V tomto případě je možné vypozorovat, jak je hluk vysoce eliminován městskou zástavbou. Samozřejmostí je i eliminace způsobená zelení, kde však záleží na hustotě a rozloze zalesnění. Na obrázku 2 je prezentována fuzzifikovaná vrstva šíření smogu od komunikace. Stejně jako v předchozím případě se jedná o šíření s překážkou, kdy překážku tvoří zeleň a zastavěná část města Bzenec. Černá barva opět znázorňuje vysokou míru smogu, která je zřetelná zejména v bezprostřední vzdálenosti komunikace R55. Na eliminaci smogu má velký vliv zeleň, která se nachází v těsné blízkosti komunikace, jak je vidět na obrázku. Na rozdíl od šíření hluku, který s rostoucí vzdáleností lineárně klesá, jak je psáno výše, smog se v případě volného prostředí šíří atmosférou mnohem dál. Zde je však třeba podotknout, že záleží například na povětrnostních podmínkách, které nejsou do analýzy započteny.
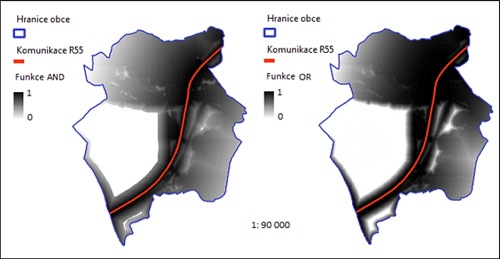
Pomocí nástroje překrytí (overlay) je možné negativní dopady popisovaných faktorů mezi sebou porovnat. Porovnáním je možné zjistit, kde působí jaký faktor nejméně či naopak nejvíce. Nástroj překrytí tedy umožňuje analýzu možnosti příslušnosti jevu do více množin. Výsledek funkce And znázorňuje v každém pixelu tu nižší hodnotu z obou fuzzifikovaných vrstev. To znamená, že v daném bodě působí na životní prostředí tato minimální hodnota, ale ve skutečnosti se v daném bodě vyskytuje ta horší hodnota. Výsledek funkce And není v tomto případě tolik přínosný jako výsledek funkce Or. Výsledek funkce Or naopak znázorňuje maximální hodnotu z obou fuzzifikovaných vrstev. Takže v každém daném bodě působí na životní prostředí ten vyšší z obou negativních faktorů. Světlejší místa znamenají lepší stav, ale stále znázorňují tu zásadnější hodnotu negativního faktoru. Nevýhodou těchto dvou metod fuzzy přístupu oproti klasickému přístupu pomocí mapové algebry je v tom, že není možné zjistit, který ze dvou negativních faktorů v daném místě více působí. Pomocí uvedených metod je možné zjistit, kde na životní prostředí působí negativní faktor s minimální či maximální hodnotou, ale již nenese informaci o tom, který negativní parametr je který. Metody zvolí buď lepší z obou dvou hodnot, popř. tu horší z obou hodnot.
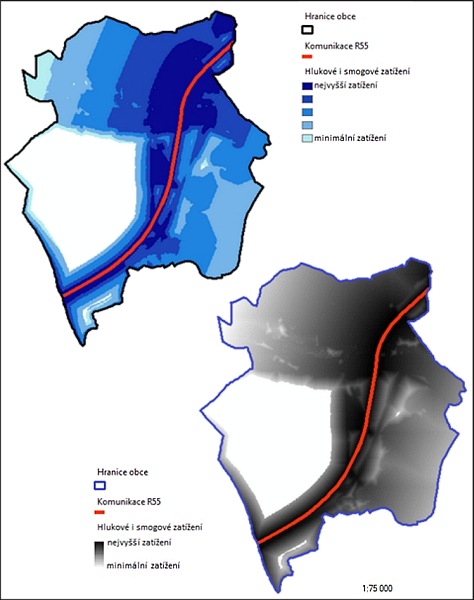
Stěžejním rozdílem je tedy to, že klasický přístup pomocí třídění vytvoří ostré hranice přechodu, ale naopak fuzzy přístup vytvoří přechody plynule. Za pomoci mapové algebry je vypočítána diference výše jmenovaných vrstev. Vzájemným odpočtem je zjištěno, kde je největší rozdíl mezi klasickým přístupem a fuzzy přístupem. Je tedy zjištěna největší disproporce mezi dvěma hodnotami (viz obrázek 5).
ZávěryV krajině se běžně vyskytuje mnoho prostorových fenoménů, u kterých lze jen stěží určit přesnou hranici výskytu. V prostorových analýzách v geografických IT tak dochází k nepřesným výsledkům. Za použití těchto nepřesných výsledků pak mohou být provedena závažná rozhodnutí s nevratným dopadem jak na krajinu, tak i na samotné obyvatele. Článek ukazuje uplatnění teorie fuzzy množin při řešení konkrétních problémů. Využití fuzzy množin může být prospěšné v různých oblastech reálného života. Teorie fuzzy množin existuje již od 60. let 20. století a v několika oblastech je již využívána. Její výhoda oproti klasické teorii množin spočívá ve schopnosti zaznamenat vágní (nepřesné) pojmy, které lidé hojně v přirozeném jazyce používají. Jádrem článku je aplikace principů fuzzy množin na vybrané prostorové ukazatele z oblasti životního prostředí zvoleného regionu jižní Moravy. Nad klasicky uloženými geodaty jsou provedeny prostorové analýzy, kde můžeme sledovat přesně vymezené hranice výskytu. V případě šíření smogu z dopravy od silniční komunikace bychom za použití klasicky uložených geodat mohli říci, že jeden dům není smogem postižen vůbec, ale sousední dům již postižen je. Klasický přístup používá ostré hranice přechodu, které nevystihují věrně realitu. V porovnání s analýzami nad fuzzifikovanými geodaty, které umožňují zachytit šíření smogu reálněji, je možné na základě funkce příslušnosti říci, v jaké míře je smogem postižena každá oblast. LiteraturaHBH Projekt, ŘSD. Rychlostní silnice R55. [on-line]. 2005. [cit. 18. 5. 2012]. Dostupné na: |











 Geografické informační technologie (GIT) modelují geografický prostor kolem nás. Využívají stávající schopnosti informačních a komunikačních technologií. K ukládání a zpracování dat vychází z klasické teorie množin, která pracuje s dvouhodnotovou logikou (1, 0). Neumí zachytit stavy mezi tím, nezná neurčitost. K zachycení neurčitosti, která je běžně obsažena v lidské řeči, vznikla teorie fuzzy množin. Slovo fuzzy lze přeložit jako neostrý, neurčitý, nejasný či vágní. Je možné se při překladu setkat i s pojmem „mlhavá logika".
Geografické informační technologie (GIT) modelují geografický prostor kolem nás. Využívají stávající schopnosti informačních a komunikačních technologií. K ukládání a zpracování dat vychází z klasické teorie množin, která pracuje s dvouhodnotovou logikou (1, 0). Neumí zachytit stavy mezi tím, nezná neurčitost. K zachycení neurčitosti, která je běžně obsažena v lidské řeči, vznikla teorie fuzzy množin. Slovo fuzzy lze přeložit jako neostrý, neurčitý, nejasný či vágní. Je možné se při překladu setkat i s pojmem „mlhavá logika".