Partneři Projektu CAD
| Po | Út | St | Čt | Pá | So | Ne |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
- 02.03. AutoCAD – kurz pro pokročilé
- 02.03. Autodesk Fusion 360 – základní kurz (úvod do parametrického modelování)
- 02.03. AutoCAD kurz – navrhování a správa dynamických bloků
- 03.03. Autodesk Fusion 360 – pro uživatele Autodesk Inventor
- 04.03. AutoCAD a AutoCAD LT – základní kurz
- 05.03. AutoCAD 2013 - základní kurz
- 05.03. workshop Strukturální mechanika v programu COMSOL Multiphysics
- 09.03. Autodesk Inventor – návrh trubek a potrubí (Tube and Pipe Design)
- 09.03. Trimble SketchUp – prezentace návrhů
- 10.03. Autodesk Inventor – kurz pro pokročilé (sestavy a strojní návrhy)
Aktuality
- AI na veletrhu HANNOVER MESSE: Od teorie k praxi
- Dassault Systèmes jmenuje nového předsedu představenstva
- HTC VIVERSE spouští nový VIVERSE Partner Program
- FinalWire vydává software AIDA64 v8.25
- Zoo představuje Zookeeper Agent pro CAD návrh
- Pevně zakódovaná budoucnost autonomních továren
- Dell Technologies a McLaren Racing prodlužují spolupráci
- Co je nového v SOLIDWORKS PDM
Možnosti modelování „self contactu" v MKP programech v rámci analýzy hadicových dopravníků |
| Autor článku: Gabriel Fedorko | |
| Neděle, 11 Listopad 2012 00:00 | |
|
Definování tohoto typu kontaktu může podle použitého softwarového nástroje způsobovat různé problémy nebo dokonce u určitých použitých programů bude řešení takového typu úlohy zcela nemožné. „Self contact" v programu AbaqusProgram Abaqus patří v současnosti mezi skupinu programů, které umožňují snadné definování „self contactu". V rámci tohoto programu dochází při definování „self contactu" k internímu generování kontaktních prvků pro každý uzel, který se nachází na ploše, kde tento druh kontaktu vzniká. V důsledku toho tak každý jeden uzel dané plochy plní současně roli „Master" a také „Slave".
Program Abaqus umožňuje definování „self contactu" u různých typů inženýrských problémů. Jedním z typických příkladů jsou úkoly, které jsou řešeny pomocí modulu Abaqus Explicit. Tento modul pro řešení jednotlivých zadání využívá explicitní metody integrování.Explicitní metoda konečných prvků se v poslední době v praxi používá stále častěji. Souvisí to především s rychlým rozvojem výpočetní techniky a s potřebami průmyslových podniků dosáhnout lepších výsledků v kratším čase. Explicitní MKP je určena pro rychlé a silně nelineární procesy. Uplatnění proto nachází například při simulaci crash-testů automobilů nebo při výpočetním modelování technologických operací.
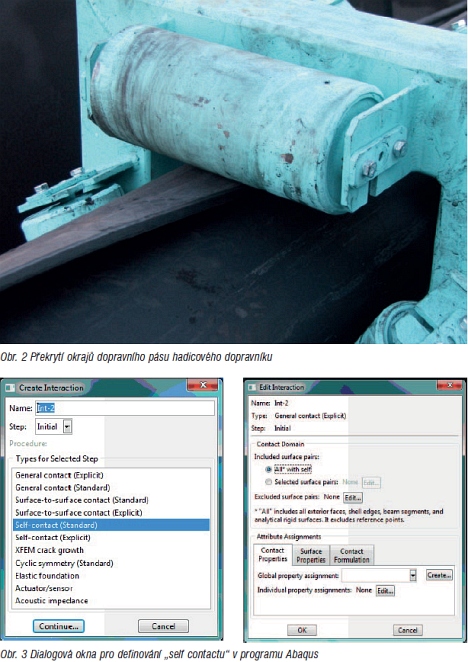
Definování „self contactu" v programu AbaqusV rámci výzkumu hadicových dopravníků na F BERG TU v Košicích byla jako jedna z výzkumných metodik použita metoda počítačové simulace, konkrétně se realizovala analýza pomocí metody konečných prvků. Pro její realizaci jsme při tvorbě výpočetního modelu v rámci vymezení kontaktních podmínek potřebovali nadefinovat „self contact", který vzniká v důsledku vzájemného překrytí okrajů dopravního pásu. Program Abaqus umožňuje definovat „self contact" dvěma způsoby. První možností je přímé definování „self contactu" pomocí dialogového okna „Create interaction" (obr. 3). Pro druhý způsob definování „self contactu" v programu Abaqus byla použita volba „General contact" v dialogovém okně „Create interaction" (obr. 3). Po jejím potvrzení se nám následně otevřelo dialogové okno „Edit interaction", ve kterém jsme zaškrtli volbu „All* with self". Volba „General contact" umožňuje zadat kontakt komplexně pro celý model a výběrem možnosti „All* with self" pracuje i se „self contactem". Při aplikaci „General contact" však musíme mít na paměti, že v rámci modelu již není možné aplikovat žádný další typ kontaktu. Nadefinování „self contactu" v programu SolidWorks Simulation
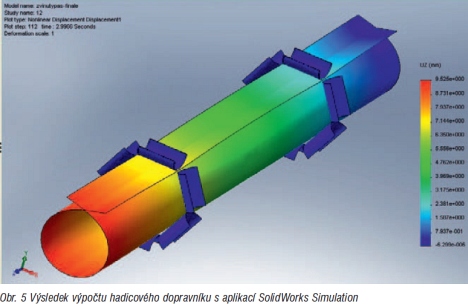
Z takto vytvořeného výpočetního modelu jsme získali výsledek, který je znázorněn na obr. 5. z obrázku je na první pohled viditelný fakt, že v průběhu výpočtu „self contact" nebyl vytvořen. Stejný výpočet jsme realizovali také s modelem vytvořeným z prvků typu solid, přičemž výsledek byl stejný jako při prvním výpočtu, kde byl použit model vytvořený z prvků typu shell.
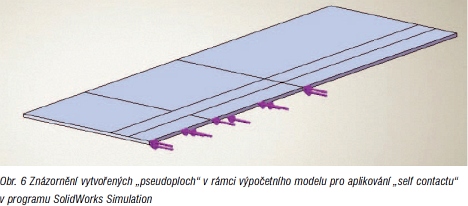
Druhý postup tvorby výpočetního modelu dopravního pasu hadicového dopravníku, který jsme se rozhodli realizovat, byl modifikací prvního neúspěšného pokusu. V rámci tohoto postupu jsme plochu dopravního pásu rozdělili na několik menších „pseudoploch" (obr. 6). Záměrem této úpravy bylo usnadnit programu identifikaci jednotlivých kontaktních dvojic. Nadefinování kontaktu jsme následně tak jako v prvním případě realizovali klasickým postupem.
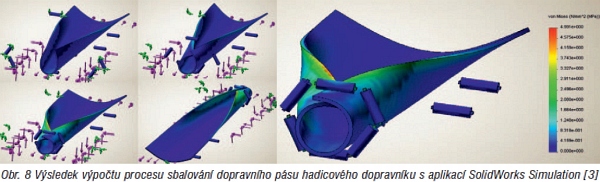
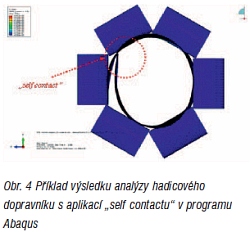
S takto vytvořeným výpočetním modelem jsme realizovali výpočet, jehož výsledek je zobrazen na obr. 7. Z prezentovaného výsledku výpočtu vyplývá, že rozdělení plochy geometrického modelu dopravního pásu umožnilo úspěšné vytvoření „self contactu". Výsledek výpočtu tak poskytuje informace o velikosti deformaci ve sbaleném dopravním pásu hadicového dopravníku s akceptací vzájemné interakce obou okrajů dopravního pásu. Velmi dobře je mimo jiné možné pozorovat vznik vyboulení, které se nachází uprostřed mezi dvěma válečkovými stolicemi (obr. 7). Pro ověření postupu, který pro vytvoření „self contactu" využívá rozdělení povrchu geometrického modelu dopravního pásu hadicového dopravníku na několik „pseudoploch", jsme vytvořili i druhý typ výpočetního modelu. V rámci tohoto modelu jsme simulovali proces postupného sbalování dopravního pásu do tvaru hadice. Pro definování „self contactu" byly znovu vytvořeny „pseudoplochy". Výsledek výpočtu a jeho postupný průběh je znázorněn na obr. 8.
Článek je součástí řešení grantového projektu VEGA 1/0922/12, VEGA 1/0184/12 a projektu VEGA 1/0036/12. Literatura[1] http://ozenapps.appspot.com/class/structural-nonlinearities/
Mohlo by vás zajímat:
|











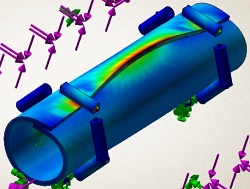 Pod pojmem „self contact" rozumíme v oblasti tvorby výpočetních modelů pro nejrůznější analýzy pomocí metody konečných prvků (MKP) takový typ úlohy, kdy je nezbytné definovat kontakt, který vzniká v důsledku vzájemné interakce „součástky samé se sebou". Uvedený typ kontaktu může vzniknout například v důsledku ohybu modelované součástky, případně v důsledku deformace tvarově složité součástky (obr. 1).
Pod pojmem „self contact" rozumíme v oblasti tvorby výpočetních modelů pro nejrůznější analýzy pomocí metody konečných prvků (MKP) takový typ úlohy, kdy je nezbytné definovat kontakt, který vzniká v důsledku vzájemné interakce „součástky samé se sebou". Uvedený typ kontaktu může vzniknout například v důsledku ohybu modelované součástky, případně v důsledku deformace tvarově složité součástky (obr. 1).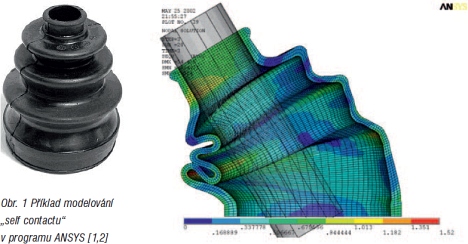
 Druhým softwarem, který byl použit pro tvorbu výpočetních modelů, byl SolidWorks Simulation. Při tvorbě modelu pomocí tohoto softwaru jsme však museli vyřešit problém, jak postupovat, abychom v rámci výpočtu měli namodelovaný „self contact", který, jak již bylo zmíněno, vzniká vzájemným překrytím obou konců dopravního pásu, protože SolidWorks Simulation nenabízí přímou možnost pro definování tohoto typu kontaktu.
Druhým softwarem, který byl použit pro tvorbu výpočetních modelů, byl SolidWorks Simulation. Při tvorbě modelu pomocí tohoto softwaru jsme však museli vyřešit problém, jak postupovat, abychom v rámci výpočtu měli namodelovaný „self contact", který, jak již bylo zmíněno, vzniká vzájemným překrytím obou konců dopravního pásu, protože SolidWorks Simulation nenabízí přímou možnost pro definování tohoto typu kontaktu.