Partneři Projektu CAD
- 05.02. AutoCAD 2013 - základní kurz
- 05.02. workshop Strukturální mechanika v programu COMSOL Multiphysics
- 09.02. Autodesk Inventor – základní kurz
- 09.02. AutoCAD Electrical – základní kurz
- 10.02. Autodesk Inventor – kurz iLogic
- 10.02. Autodesk Inventor – kurz iLogic
- 11.02. Autodesk Inventor – návrh plechových dílů a součástí (Sheet Metal Design)...
- 12.02. AutoCAD – kurz pro středně pokročilé
- 13.02. Autodesk Inventor – kurz iLogic
- 16.02. AutoCAD a AutoCAD LT – základní kurz
Aktuality
- Řešení pro reverzní inženýrství v oblasti aditivní výroby od Authentise
- Partnerství NVIDIA a Dassaultu pro průmyslová virtuální dvojčata
- Česká stopa v Artemis II: Astronauti NASA se po 53 letech vrací k Měsíci
- InfinitForm spouští generativní inženýrskou platformu
- Budoucnost designu a výroby na 3DEXPERIENCE World 2026
- eQuorum vydává ImageSite, EngineBox verze 12.3
- Integrace 2D a 3D konstrukčních dat mění moderní návrh zařízení
- Partnerství TriMech Group a Capone Motorsports
Modul Grasshopper |
| Čtvrtek, 24 Červen 2010 08:37 | |
|
pro vizuální parametrické programování ve Rhinu  Programováním jsem téměř nedotčen (pokud nepočítám jazyk Karel na IQ 151 a několik úvodních kapitol Pascalu) a jakýkoliv text s očíslovanými řádky a nenulovým výskytem špičatých závorek se pro mě stává krajně podezřelým. Jak je tedy možné, že jsem nedávno programovat začal a dokonce mě to baví víc než samotné modelování? Odpovědí je zásuvný modul Grasshopper pro 3D modelář Rhinoceros, který umožňuje tvořit interaktivní „programy“ bez napsání jediné čárky kódu. A navíc si ho můžete stáhnout zcela zdarma. Generativní modelováníPokud vás zajímá, jak snadno se v Grasshopperu (pro úsporu místa dále jen GH) dá vytvářet plně parametrický a interaktivní grafický program (nazývá se také generativní model), nainstalujte si nejprve Rhino (postačí i demoverze), stáhněte si GH z domovské stránky Grasshopper3D.com a pusťte se do krátkých návodů v tomto článku. Uvidíte, jak nečekaně snadné to je. 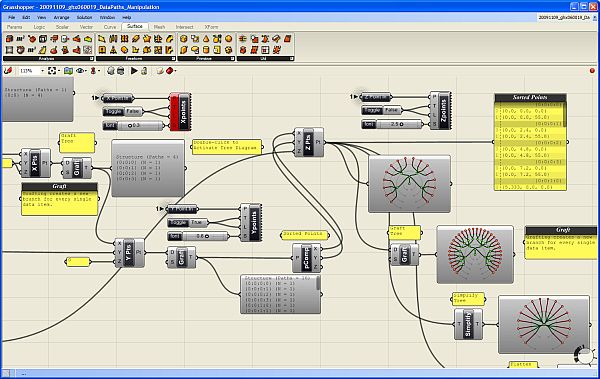 Uspořádání okna GrasshopperuKdyž nainstalujete GH a spustíte Rhino, stačí do příkazového řádku zadat Grasshopper a stisknout Enter a spustí se vlastní editor GH. V horní části okna se nachází roletové menu a hned pod ním jsou uspořádány veškeré příkazy GH do logických celků, které můžete přepínat pomocí záložek. Při klepnutí na danou záložku se zobrazí ikony, které jsou opět rozděleny do skupin. Editor obsahuje tyto záložky: Params (vkládání parametrů a ovládacích prvků), Logic (logické operace), Scalar (skalární operace), Vector (vektorové operace), Curve (tvorba a editace křivek), Surface (tvorba a editace ploch), Mesh (tvorba a editace polygonových sítí), Intersect (řešení přůsečíků mezi objekty) a XForm. Když na nějaké ikoně podržíte na zlomek sekundy myš, objeví se její název a stručný popis. Typy definičních objektůPrvky na plátně (tedy ony „integrované obvody“) rozdělujeme do dvou základních skupin – komponenty a parametry. Komponenty provádějí akci, to znamená, že něco vykonávají. Je to vlastně obdoba příkazů Rhina. Parametry obsahují data, to znamená, že něco ukládají, nesou nějakou geometrickou informaci (zastupují skutečně existující křivku, plochu, bod nebo polygonovou síť v modelu Rhina) nebo hodnotu (numerickou, logickou atd). Představme si například komponentu s názvem „Cir“ (zkratka příkaz Circle neboli Kružnice), která vytvoří kružnici na základě zadaného bodu (středu), normálového vektoru a poloměru. Má tři vstupní parametry s názvy C, N a R (zkratky slov Center, Normal a Radius, česky střed, normála a poloměr) a jeden výstupní parametr s názvem C, který uchová výstupní kružnici. Všechny názvy lze změnit na více popisné, ale standardní komponenty jsou záměrně z hlediska popisu minimalistické kvůli šetření místem na obrazovce. Při výběru komponenta zežloutne. 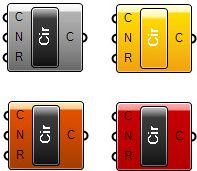 Kdykoliv se komponenta (nebo parametr) změní na oranžovou nebo červenou, najdete o tom v menu další informace. Informace o varování nebo chybě bude trvale zobrazena až do pokusu o nové řešení, což je obvykle okamžik, kdy v Definici změníte propojení nebo strukturu dat. Pokud touto změnou dojde k vyřešení problému, vrátí se barvy zpět do normálu. Barva výběru ale má vyšší váhu než barva varování nebo chyby. Je to vlastně stejné, jako když modelujete – pokud chcete například rozdělit křivku na určitý počet dílků, spustíte odpovídající příkaz a Rhino vás nejprve vyzve k výběru křivky a poté k zadání počtu dílků, které mají na křivce vzniknout. V GH je to stejné – do vstupu Curve (křivka) připojíte výstup parametru, který obsahuje skutečnou křivku v pohledu Rhina, a ve vstupu Number nadefinujete počet požadovaných dílků. V pohledu Rhina pak dojde automaticky k rozčlenění zvolené křivky na požadovaný počet dílků, jak za chvíli uvidíte v našem příkladu. Datové typyParametry se používají pouze jako nosiče informací, ale většina parametrů dokáže uchovávat dva různé druhy dat – dočasná (volatile) a trvalá (persistent). Dočasná data jsou zděděna z jednoho nebo více zdrojových parametrů pomocí propojení a jsou zničena (neboli znovu získána) při každém spuštění nového řešení. Trvalá data jsou data, která byla výslovně zadána uživatelem. Když je parametr připojen ke zdrojovému objektu, budou data ignorována, ale nebudou zničena. Výjimkou jsou výstupní parametry, které nemohou uchovávat trvalé záznamy ani definovat množinu zdrojů. Výstupní parametry jsou plně pod kontrolou komponenty, která je vlastní.Trvalá data jsou přístupná skrze kontextové menu po klepnutí pravým tlačítkem myši na daný parametr a v závislosti na druhu parametru mají různého správce, například číselné parametry umožní nastavit jednu hodnotu v menu (rychlý a snadný způsob) nebo můžete použít Generic Value Manager pro zadání, změnu a přeskupení série čísel. Správa propojeníProtože parametry jsou v péči svých vlastních datových struktur, můžete k těmto nastavením získat přístup prostřednictvím daného parametru. To je důležité. Propojení jdou PROTI toku dat. Propojení indikuje, kterým zdrojům parametr „naslouchá“, nikoliv které parametry závisí na zdroji. Pokud chcete vytvořit nové propojení, musíte táhnout nový propojovací „drát“ z levé strany cílového parametru na pravou stranu zdrojového parametru.Předpokládejme, že máme komponent Point (Bod), který z hodnot X, Y a Z zkonstruuje 3D bod a my tento parametr chceme připojit k nějakým „poskytovatelům“ souřadnic:  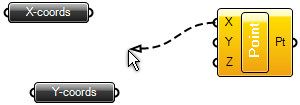 Jakmile se myš (se stisknutým levým tlačítkem) ocitne na pozici potenciálního zdroje parametru, změní se drát na plnou čáru. Toto spojení není trvalé do té doby, než pustíte myš:  Nové propojení z téhož vstupu standardně zruší již existující propojení. Protože je předpoklad, že nejčastěji budete používat pouze jednoduchá propojení, musíte pro definici více zdrojů udělat něco navíc. Pokud při tažení propojovacího drátu podržíte Shift nebo Ctrl, změní se ukazatel myši tak, že vám dá prostřednictvím zkratky ADD (přidat) nebo REM (odebrat) najevo, zda proběhne přidání nebo smazání propojení: 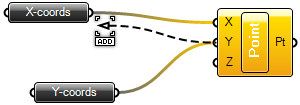 Pokud je v okamžiku uvolnění tlačítka myši aktivní kurzor s nápisem „ADD“, bude daný parametr přidán do seznamu zdrojů. Pokud specifikujete parametr, který je již definován jako zdroj, nic se nestane. Z jednoho zdroje nemůžete zdědit data více než jednou. Pokud je u kurzoru nápis „REM“, cílový zdroj bude ze seznamu zdrojů odstraněn. Pokud cíl není odnikud odkazován, nic se neprovede. 1. úloha – „zakřivený žebřík“V tomto příkladu si vytvoříme „žebřík“ mezi dvěma obecnými křivkami tak, že je rozdělíme na stejný počet dílků a tyto dílky navzájem propojíme příčnými úsečkami. Nejdříve si pomocí nástroje Křivka nakreslíme dvě obecné otevřené křivky (počet řídicích bodů ani tvar křivky není omezen, v rámci rozumného výsledku by ale bylo vhodné, aby křivky byly tvarově podobné) a příkazem Grasshopper spustíme stejnojmenný modul. Prvním krokem tvorby definice v Grasshopperu je vložení křivek, které jsme si nakreslili ve Rhinu, do programové definice na plátně Grasshopperu. V horizontální řadě ikon Grasshopperu si přepněte záložku Params, klepněte na skupinu nástrojů Geometry (nejlépe přímo na černý pruh s tímto nápisem) a rozbalí se nabídka všech nástrojů v této skupině. Zvolte nástroje Curve a přesuňte jej na plátno. Provedete to buď tak, že na nástroj klepnete a poté klepnete do plátna, nebo jej uchopíte myší a přetáhnete jej na plátno. Výsledek je v obou případech totožný – na plátně se objeví parametr Crv (zkratka slova curve – křivka).  Má oranžovou barvu, protože zatím není definován jeho obsah. Klikněte na něj pravým tlačítkem myši a objeví se kontextové menu, ve kterém můžete hned v prvním políčku změnit název tohoto parametru, abyste se v definici lépe orientovali. Nazvěte si jej třeba Křivka 1. Teď musíme definovat obsah tohoto parametru – musíme dát Grasshopperu nějak najevo, že parametr Křivka 1 bude zastupovat reálnou křivku z naší scény v Rhinu. Provedete to tak, že na parametr Křivka 1 kliknete opět pravým tlačítkem myši a v menu zvolíte položku Set one Curve (vybrat jednu křivku). 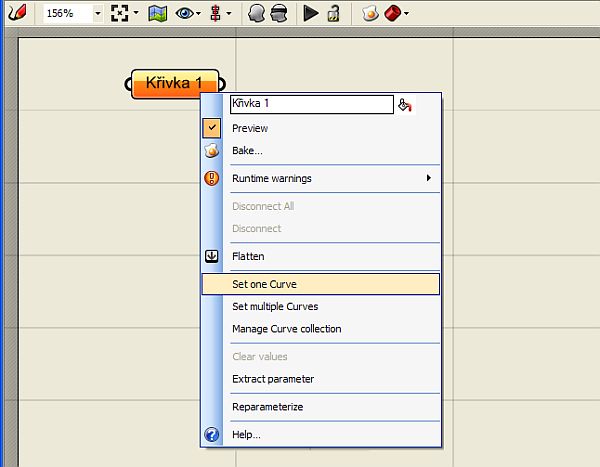 Grasshopper na chvíli zmizí a vy můžete ve Rhinu vybrat jednu ze dvou křivek, kterou jste si před chvílí nakreslili. Až křivku vyberete, vrátíte se ihned do Grasshopperu. Klepněte myší někam do prázdné plochy plátna a všimněte si, že parametr je nyní zobrazen černou barvou, na znamení toho, že již nese nějaký obsah. 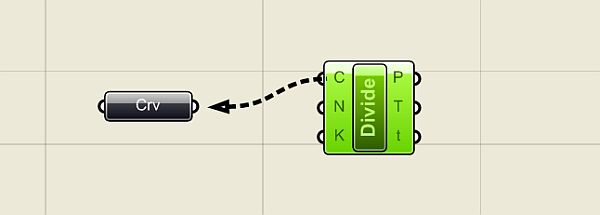 Jakmile pustíte myš, všimněte si, co se stane s vaší křivkou – vygenerovaly se na ní body, které ji rozdělily na 10 stejně dlouhých částí. Ale proč zrovna 10? Odpověď hledejme ve výchozím nastavení vstupu N v příkazu Divide. Klepněte pravým tlačítkem myši na vstup „N“ tohoto příkazu a v roletovém menu vyberte položku Set integer. Rozvine se podmenu s numerickým políčkem, ve kterém je standardně zadána hodnota 10. Zkuste ji změnit a sledujte, co se stane s křivkou. Vraťte zpět hodnotu 10 a nakonec najeďte myší na výstup „P“ (bez stisknutí tlačítka). 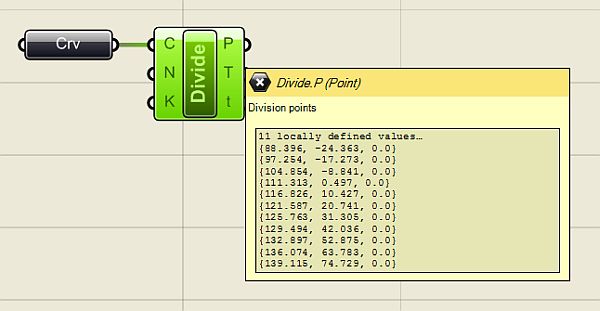 Jak již bylo řečeno výše, jedná se o souřadnice vygenerovaných bodů na křivce. Protože jsem obě křivky nakreslil v rovině XY, je souřadnice Z u všech bodů nulová, ale naše definice bude samozřejmě fungovat na jakékoliv 3D prostorové křivky. 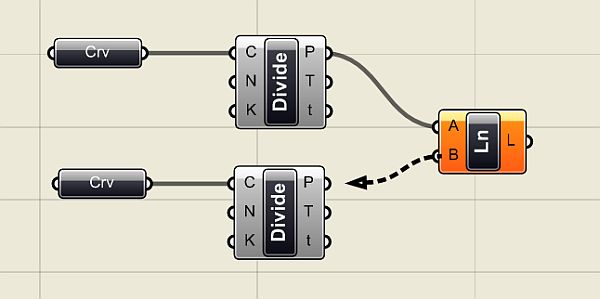 Výsledkem bude okamžité propojení bodů na křivkách úsečkami. Zkuste křivky přesunovat a klávesou F10 si zobrazte jejich řídicí body a deformujte křivky přesunováním těchto řídicích bodů (zkuste také klávesy Alt + kurzorové šipky pro přesun bodů v krocích). To je skvělý rys Grasshopperu – veškeré změny v modelu se ihned promítají do výstupu z Grasshopperu a naopak. Nyní totiž můžete nejen měnit tvar a polohu křivek, ale můžete měnit i hodnoty vstupů v definici Grasshopperu a model na tyto změny bude reagovat okamžitým překreslením. Ukážeme si to na změně vstupního parametru „N“ v příkazech Divide. Můžete samozřejmě pomocí pravého tlačítka myši a položky menu „Set integer“ zadávat nové hodnoty počtu segmentů křivky, to ale není příliš pohodlné a už vůbec ne divácky vděčné. Provedeme to jinak – v záložce Params vyberte v příkazové skupině Special položku Number Slider a umístěte ji na plátno někam mezi parametry křivek. Jak správně tušíte, tento komponent slouží k plynulé změně vstupních hodnot pomocí posuvníku. Klepněte na něj pravým tlačítkem myši a vyberte položku Slider type > Integer. Budeme totiž měnit počet segmentů křivky a to je samozřejmě celočíselná hodnota. Dále v tomtéž menu vyberte položku Edit... a v dialogovém okně, které se objeví, nastavte dolní a horní hodnotu rozsahu na 3 a 30 (podle polohy posuvníku se bude křivka dělit na 3 až 30 dílků). Jako výchozí hodnotu nastavte ve spodní části okna 10. 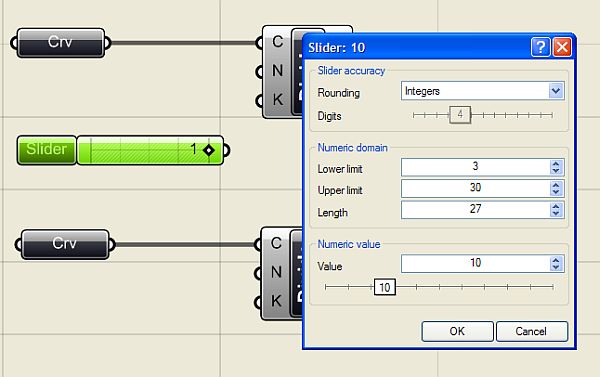 Nakonec si propojte vstupy obou příkazů Divide s výstupem posuvníku a pohybujte posuvníkem. V reálném čase se bude měnit počet bodů na křivce, a tedy i počet propojek našeho virtuálního „žebříku“. Výsledek můžete navíc ještě ovlivňovat přesunováním a deformací vstupních křivek. 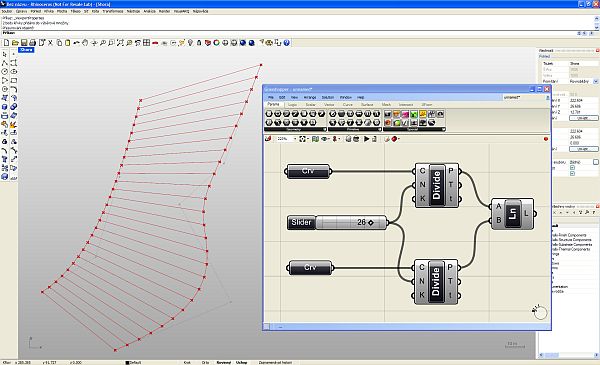 Vidíte, že „programování“ v Grasshopperu je záležitost značně jednoduchá a zábavná. Teď se podíváme na trochu komplikovanější případ, budeme v reálném čase provádět metamorfózu mezi dvěma obecnými plochami. O co složitěji to zní, o to jednodušší bude řešení této úlohy. 2. úloha – středová plocha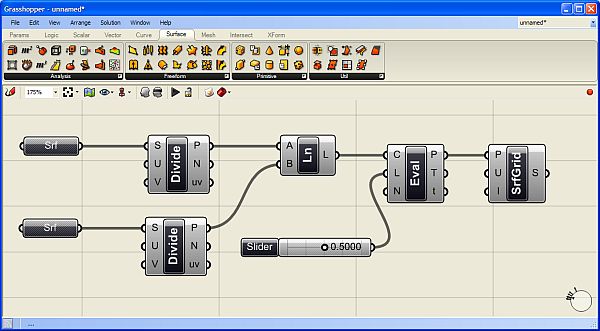 Protože jste již zkušení uživatelé GH, podívejte se na výslednou definici a obrázky výstupů. Na prvním obrázku je výsledná (červená) plocha přesně uprostřed mezi dvěma vstupními plochami, na druhém je pomocí posuvníku přesunuta blíže k dolní ploše a zároveň byl pomocí řídicích bodů upraven tvar vstupních ploch. Účinek všech těchto změn přitom vidíte okamžitě, protože výsledná plocha se překresluje v reálném čase.  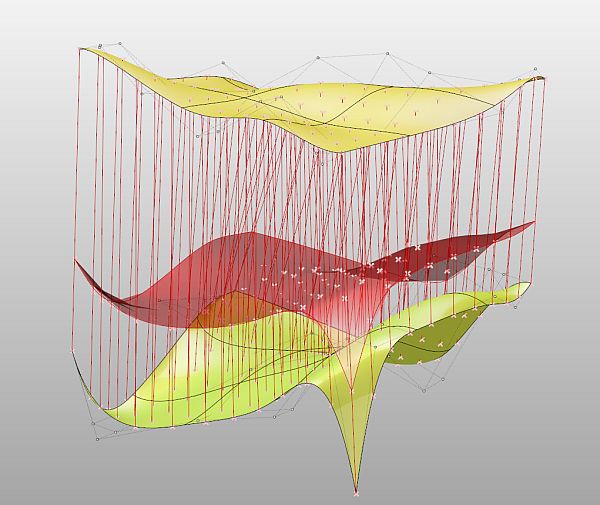 Poté si můžete prohlédnout podrobný rozbor tvorby programu v českém videonávodu, jehož internetovou adresu najdete u tohoto článku. Přeji vám hodně zábavy při experimentování s Grasshopperem.
Mohlo by vás zajímat:
|