Partneři Projektu CAD
- 09.02. Autodesk Inventor – základní kurz
- 09.02. AutoCAD Electrical – základní kurz
- 10.02. Autodesk Inventor – kurz iLogic
- 10.02. Autodesk Inventor – kurz iLogic
- 11.02. Autodesk Inventor – návrh plechových dílů a součástí (Sheet Metal Design)...
- 12.02. AutoCAD – kurz pro středně pokročilé
- 13.02. Autodesk Inventor – kurz iLogic
- 16.02. AutoCAD a AutoCAD LT – základní kurz
- 19.02. Trimble SketchUp – základní kurz
- 19.02. workshop Strukturální mechanika v programu COMSOL Multiphysics
Aktuality
- Siemens získává Canopus AI pro zrychlení výroby polovodičů
- CATIA V5 v roce 2026: stabilní základ, nebo brzda dalšího rozvoje?
- Řešení pro reverzní inženýrství v oblasti aditivní výroby od Authentise
- Partnerství NVIDIA a Dassaultu pro průmyslová virtuální dvojčata
- Česká stopa v Artemis II: Astronauti NASA se po 53 letech vrací k Měsíci
- InfinitForm spouští generativní inženýrskou platformu
- Budoucnost designu a výroby na 3DEXPERIENCE World 2026
- eQuorum vydává ImageSite, EngineBox verze 12.3
Modelování napěťově-deformačních stavů v dopravních pásech klasických pásových dopravníků |
| Autor článku: Gabriel Fedorko – Matúš Beluško | |
| Čtvrtek, 15 Listopad 2012 00:00 | |
|
V procesu návrhu pásových dopravníků mají tyto informace rozhodující podíl při návrhu pohonu dopravníku a volbě dopravního pásu vhodné konstrukce. Tato skutečnost značně ovlivňuje provozní náklady, ale v neposlední řadě má vliv i na životnost dopravního pásu a výrazně ji ovlivňuje. Dopravní pásDopravní pás je z hlediska provozu dopravníku jeho nejdůležitější částí. Je to uzavřený prvek obíhající kolem koncových bubnů, který při svém oběhu plní funkci nesení materiálu, břemen nebo osob na přepravní délce a současně plní funkci tažného prvku a přenáší všechny odpory, vznikající při jeho pohybu.
Kostra dopravního pásu slouží k přenosu tažných sil z hnacího bubnu na dopravní pás, zabezpečuje mu potřebnou pevnost a protirázovou odolnost. Horní krycí vrstva spolu s okrajem chrání kostru proti jejímu mechanickému poškození přepravovaným materiálem, proti působení vlhkosti i proti chemickým a termickým vlivům působícím na dopravní pás. Dolní krycí vrstva přichází do kontaktu s bubny a válečky dopravníku a chrání kostru před jejich negativními účinky. Důležitá je adheze krycí vrstvy s kostrou, protože zajišťuje přenos hnacího momentu bubnu na celý dopravní pás [1]. Tvorba výpočetního modeluPro potřeby počítačové analýzy byl navržen a vytvořen výpočetní model, který reprezentuje úsek na výsypném konci pásového dopravníku. V rámci tohoto úseku dochází k postupnému transformování dopravního pásu z korýtkového do plochého tvaru. Geometrie výpočetního modelu byla vytvořena pomocí preprocesoru programu Abaqus. Geometrie výpočetního modeluPodpěrný váleček v rámci výpočetního modelu byl vytvořen vytažením s poloměrem základny 66,5 mm a délkou 465 mm. Následně byl váleček podélně rozdělen na horní a dolní část. Dolní část válečku byla pro zjednodušení výpočtu odstraněna. Vytažením/extrudováním byl vytvořen i dopravní pás. Šířka pásu v rámci modelu je 1200 mm a tloušťka 6,8 mm. Pás byl rozdělen na jednotlivé pseudoplochy, které přicházejí do styku s válečky, čímž se z hlediska kontaktních podmínek výpočet zjednodušil.
V modulu „Assembly" byla pomocí funkcí „linearn pattern", „translate instance" a „rotate instance" vytvořena část dopravníku (obr. 3), která sestává z dopravního pásu a tří válečkových stolic. Vzdálenosti mezi válečky byly definovány 10 mm na šířku a 1220 mm na délku. Na konci pásu je umístěna část vratného bubnu o poloměru 200 mm. Materiálové charakteristikyMateriálové vlastnosti dopravního pásu jsme v rámci výpočtu modelovali jako elastický, lamina s hustotou 1.099-009 t.mm-3, poissonovým číslem 0,499 a modul pružnosti ve smyku je 2,9 MPa. Youngův modul pružnosti v příčném směru jsme definovali 397 MPa a v podélném směru 5,4 MPa. V pásu byla definována orientace materiálových vlastností pomocí lokálního souřadnicového systému. Definování kontaktůDopravní pás je rozdělen na úseky, které přijdou do styku s válečky, čímž se zjednodušil výpočet pro Abaqus. Ze stejného důvodu jsou rozděleny i válečky v horizontálním směru. Tyto úseky jsou definovány v „Assembly" jako povrchy. Pro každý takto vytvořený úsek pásu je přidělena jemu odpovídající část válečku. Pro definované kontakty byla přiřazena stabilizace kontaktu přes „contact controls". Jako „master surface" byly definovány povrchy válečků a kladky, které určují směr a velikost pohybu. Pro „slave surface" byly přiřazeny části dopravního pásu, které přicházejí do kontaktu s jim odpovídajícím povrchem válečku. Povrchy přiřazené pro „slave surface" mají za úkol přizpůsobit se pohybu povrchů definovaných jako „master surface".
Okrajové podmínkyStředové válečky stejně jako buben mají odebrány všechny stupně volnosti. Boční válečky jsou upevněny proti pohybu v ose X a rotací v ose Y a Z. Tyto válečky mají zároveň další okrajovou podmínku, přes kterou je definována jejich rotace do požadovaného úhlu. Gravitace a napínání pásuGravitace je definována v sekci „Load" na celý model ve směru osy Y o hodnotě g = –9810 mm.s-2. Dopravní pás může být podle požadavků na začátku výpočtu, resp. během jeho průběhu zatěžován napínací silou. SíťováníPro tvorbu sítě konečných prvků byly použity prvky typu Shell. Síťování válečků je definováno konečnými prvky o velikosti 15 mm, zatímco pás má síťování vytvořené z konečných prvků o velikosti 20 mm. Menší velikost konečných prvků v rámci síťování by sice zvýšila přesnost výpočtu, ale musela by být realizována s ohledem na možnosti použitého hardwaru. Využití výpočetního modeluVýpočetní model umožňuje analyzovat proces transformace dopravního pásu z korýtkové tvaru do plochého tvaru (obr. 5). Jde o důležitý faktor, který významně ovlivňuje velikost pohybových odporů a tím i nároky na pohon pásového dopravníku. Model nám tak umožňuje identifikovat místa jejich vzniku.
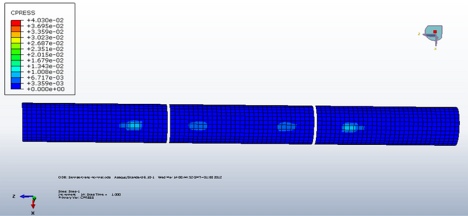
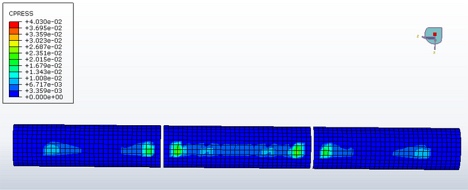
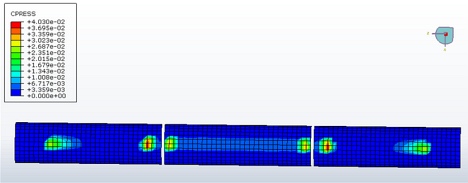
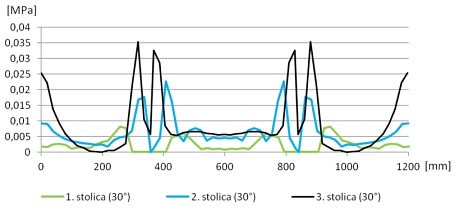
Dalším důležitým údajem, který prezentovaný výpočetní model poskytuje, jsou informace o uložení dopravního pásu ve válečkových stolicích. Můžeme se tak přesvědčit, zda je dopravní pás vhodný pro dané konstrukční řešení pásové dopravníku. Jde především o skutečnost, zda materiálové charakteristiky dopravního pásu umožňují jeho správné uložení na válečcích (obr. 6, 7).
Popsaný výpočetní model umožňuje podrobně zkoumat a analyzovat zákonitosti vzniku a existence pohybových odporů a kontaktních sil v dopravním pásu pásového dopravníku. Je vytvořen s hlavním záměrem umožnit výzkum podmínek, které ovlivňují velikost pohybových odporů a kontaktních sil při provozu pásových dopravníků. Získané výsledky lze po důkladné analýze využít pro stanovení základních postulátů pro určování velikosti provozních odporů a kontaktních sil. Poznání kontaktních sil a pohybových odporů pásových dopravníků je skutečnost, kterou je nutné znát, protože tyto ve výrazné míře ovlivňují životnost dopravních pásů.
Prodloužení životnosti dopravního pásu je tak spojeno s velkou ekonomickou úsporou, především z důvodu, že cena nových dopravních pásů je značně vysoká, představuje často neplánované náklady a výměna dopravního pásu je většinou spojena s dalšími ekonomickými ztrátami v důsledku např. odstávky technologických zařízení.
Literatura[1] Marasová, D., Taraba, V., Grujić, M., Fedorko, G., Bindzár, P., Husáková, N.: Pásová doprava. Fakulta BERG, Technická univerzita v Košiciach, Košice 2006, ISBN 80-8073-628-6
Mohlo by vás zajímat:
|










 Pásové dopravníky patří mezi nejvíce používané dopravní systémy v různých technologických procesech (obr. 1). Umožňují přepravovat materiál na různé vzdálenosti. Využívají se především na přepravu sypkých materiálů, resp. materiálů s určitou maximální kusovitostí. Z konstrukčního hlediska je pásový dopravník tvořen širokou škálou komponentů, které svými vlastnostmi výrazně přispívají k jeho efektivnímu provozu. Poznání vlivu materiálových charakteristik a technologických parametrů dopravních pásů na velikost kontaktních sil a pohybových odporů hadicových dopravníků má důležitý význam při jejich návrhu a provozování.
Pásové dopravníky patří mezi nejvíce používané dopravní systémy v různých technologických procesech (obr. 1). Umožňují přepravovat materiál na různé vzdálenosti. Využívají se především na přepravu sypkých materiálů, resp. materiálů s určitou maximální kusovitostí. Z konstrukčního hlediska je pásový dopravník tvořen širokou škálou komponentů, které svými vlastnostmi výrazně přispívají k jeho efektivnímu provozu. Poznání vlivu materiálových charakteristik a technologických parametrů dopravních pásů na velikost kontaktních sil a pohybových odporů hadicových dopravníků má důležitý význam při jejich návrhu a provozování.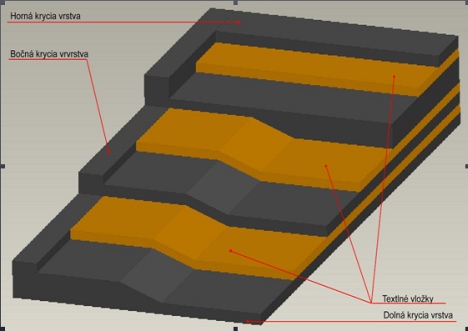
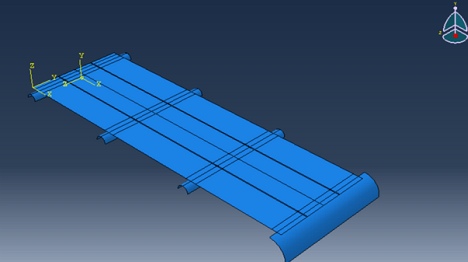
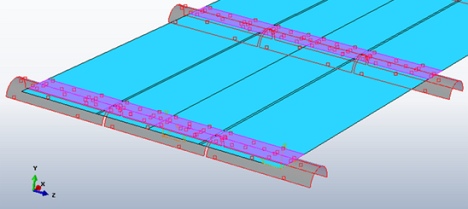
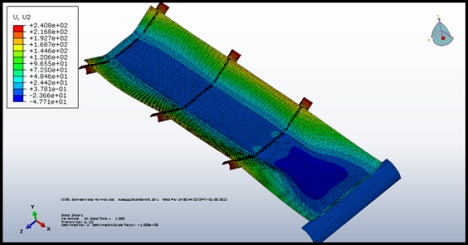

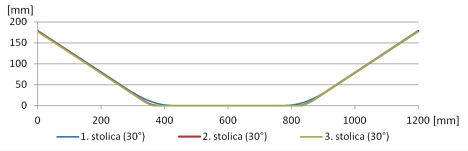 Obr. 7 Znázornění pozice pásu na válečkových stolicích při transformaci
Obr. 7 Znázornění pozice pásu na válečkových stolicích při transformaci